how to find the apothem

Apothem of a n-sided regular polygon

Given here the side length a of a regular n-sided polygon, the task is to find the length of its Apothem.
Apothem is the line drawn from the center of the polygon that is perpendicular to one of its sides.
Examples:

            Input            a = 9, n = 6            Output:            7.79424            Input:            a = 8, n = 7            Output:            8.30609

Attention reader! Don't stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course .

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

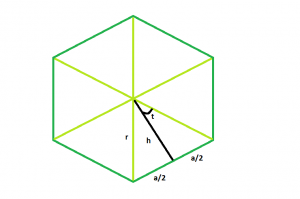
Approach:

In the figure, we see the polygon can be divided into n equal triangles.
Looking into one of the triangles, we see the whole angle at the centre can be divided into = 360/n
So, angle t = 180/n
now, tan t = a/2h
So, h = a/(2*tan t)
here, h is the apothem,
so, apothem = a/(2*tan(180/n))

Below is the implementation of the above approach.

C++

#include <bits/stdc++.h>

using namespace std;

float polyapothem( float n, float a)

{

if (a < 0 && n < 0)

return -1;

return a / (2 * tan ((180 / n) * 3.14159 / 180));

}

int main()

{

float a = 9, n = 6;

cout << polyapothem(n, a) << endl;

return 0;

}

Java

import java.util.*;

class GFG

{

double polyapothem( double n, double a)

{

if (a < 0 && n < 0 )

return - 1 ;

return (a / ( 2 * java.lang.Math.tan(( 180 / n)

* 3.14159 / 180 )));

}

public static void main(String args[])

{

double a = 9 , n = 6 ;

GFG g= new GFG();

System.out.println(g.polyapothem(n, a));

}

Python3

from math import tan

def polyapothem(n, a):

if (a < 0 and n < 0 ):

return - 1

return a / ( 2 * tan(( 180 / n) *

3.14159 / 180 ))

if __name__ = = '__main__' :

a = 9

n = 6

print ( '{0:.6}' . format (polyapothem(n, a)))

C#

using System;

class GFG

{

static double polyapothem( double n,

double a)

{

if (a < 0 && n < 0)

return -1;

return (a / (2 * Math.Tan((180 / n) *

3.14159 / 180)));

}

public static void Main()

{

double a = 9, n = 6;

Console.WriteLine(Math.Round(polyapothem(n, a), 4));

}

PHP

<?php

function polyapothem( $n , $a )

{

if ( $a < 0 && $n < 0)

return -1;

return $a / (2 * tan((180 / $n ) *

3.14159 / 180));

}

$a = 9; $n = 6;

echo polyapothem( $n , $a ) . "\n" ;

?>

Javascript

<script>

function polyapothem(n , a)

{

if (a < 0 && n < 0)

return -1;

return (a / (2 * Math.tan((180 / n)

* 3.14159 / 180)));

}

var a = 9, n = 6;

document.write(polyapothem(n, a).toFixed(5));

</script>